Modal analysis is a technique of dynamic analysis of structures. Its objective is to estimate dynamic properties such as frequencies and natural modes during free vibration as well as damping.
The Finite Element method is often used to develop the analysis because the pipes being analysed have arbitrary shapes and the results of the calculations are better. The types of equations that arise from modal analysis are seen in Eigen Systems. The physical interpretation of the Eigenvalues and Eigenvectors, which come from solving the system, represent the corresponding frequencies and modes of vibration.
According to the calculation carried out, the only desired modes are those corresponding to the lowest frequencies because they can be the predominant modes in the vibration of the pipes, and involve more mass. Thus, the modes calculated for seismic analysis will be limited to a lower frequency than those used for a water hammer.
In this way, AutoPIPE calculates the optimal distance between nodes for the frequency that we indicate and divides each element into up to 10 elements, being able to increase the number of nodes in the system up to 100,000.
The most used mass models are:
Concentrated Mass models are more efficient and accurate in finding the natural modes of vibration and the mass involved in each mode.
Consistent Mass models are faster to solve, but in the case of pipes they can be more inaccurate.
AutoPIPE distributes the mass at multiple points in the piping system and uses a Concentrated Mass model and solves it by Finite Elements with great precision.
Other programs use consistent mass methods to increase speed, but have more error.
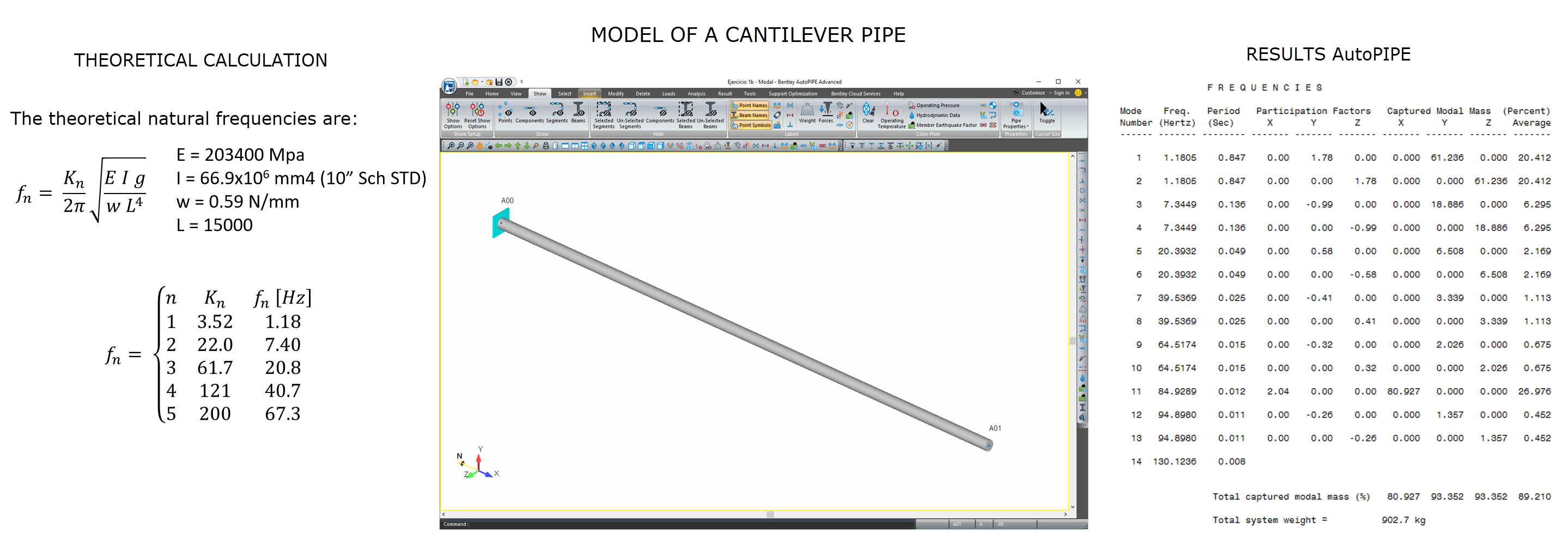
The small difference between the theoretical calculation and that of AutoPIPE is due to the fact that the theoretical calculation assumes an anchor of infinite stiffness and the AutoPIPE uses a value of 2E9 N.m / deg. Due to its accuracy, AutoPIPE is one of the two programs accepted by the NUPIC for dynamic analysis of critical nuclear facilities (The other accepted program is ANSYS ©).